[추천시스템 논문 리뷰] Matrix Factorization Techniques for Recommender Systems

디지털 서비스의 개인화에 대한 연구가 아직 무르익지 않았던 2006년, 넷플릭스는 사용자들의 영화 선호도 데이터를 기반으로 추천 시스템 공모전(Netflix Prize)을 열었다.

이 대회는 현대의 AI 공모전의 조상격이 되는 것으로, 최종 우승은 여후다 코렌(Yehuda Koren), 로버트 벨(Robert Bell)과 크리스 볼린스키(Chris Volinsky) 3인으로 구성된 벨코(BellKor)팀이 차지했다. 그들은 대회 규칙에 따라 그들의 알고리즘을 공개하였고, 이후 같은 기술을 응용한 추천 시스템이 세상을 휩쓸게 된다. 그들이 대회에서 사용했던 테크닉을 집대성한 기념비적인 논문을 살펴보자.

“추천 시스템을 위한 행렬 분해 기법”.

문제 정의

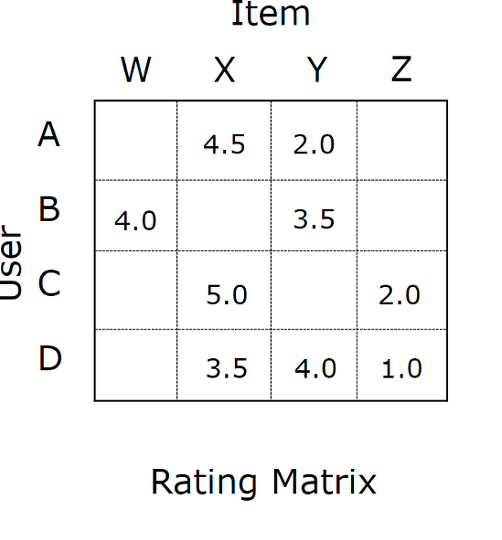
추천 시스템은 일반적으로 사용자와 상품의 상호작용을 나타낸 데이터를 다룬다. 이 데이터로 모델링을 진행하여, 학습 데이터에 존재하지 않는 사용자와 상품 사이에 어떤 상호작용이 이루어졌을지 예측하는 것이 추천 시스템의 주요 과제이다. 예를 들면 Netflix Prize 데이터는 다음과 같이 구성되어 있다.

위 데이터는 실제 Netflix Prize 데이터의 일부이다. 1행의 “1”이라는 글씨는 사용자 번호이고, 아래 행들의 숫자들은 각각 영화 번호, 1번 사용자가 그 영화에 부여한 평점, 그리고 평점 부여 시각이다. 이제 아래 데이터를 보자.

위 데이터는 실제 Netflix Prize 데이터의 일부를 캡쳐해 평점을 삭제한 것이다. 이렇게 비공개된 평점을 예측하는 것이 우리에게 주어진 과제이다. 실제 대회에서는 예측한 평점과 실제 정답의 Mean Squared Error가 평가 지표로 선택되었다.

Matrix Factorization

위의 원본 데이터를 토대로, 사용자와 상품 사이의 상호작용을 나타내는 거대한 상호작용 행렬(Interaction Matrix)을 생각해볼 수 있다. 모든 사용자가 모든 상품을 열람했을 확률은 매우 낮으므로, 이 행렬은 군데군데 빈칸이 뚫린 희소 행렬(Sparse Matrix)일 것이다.

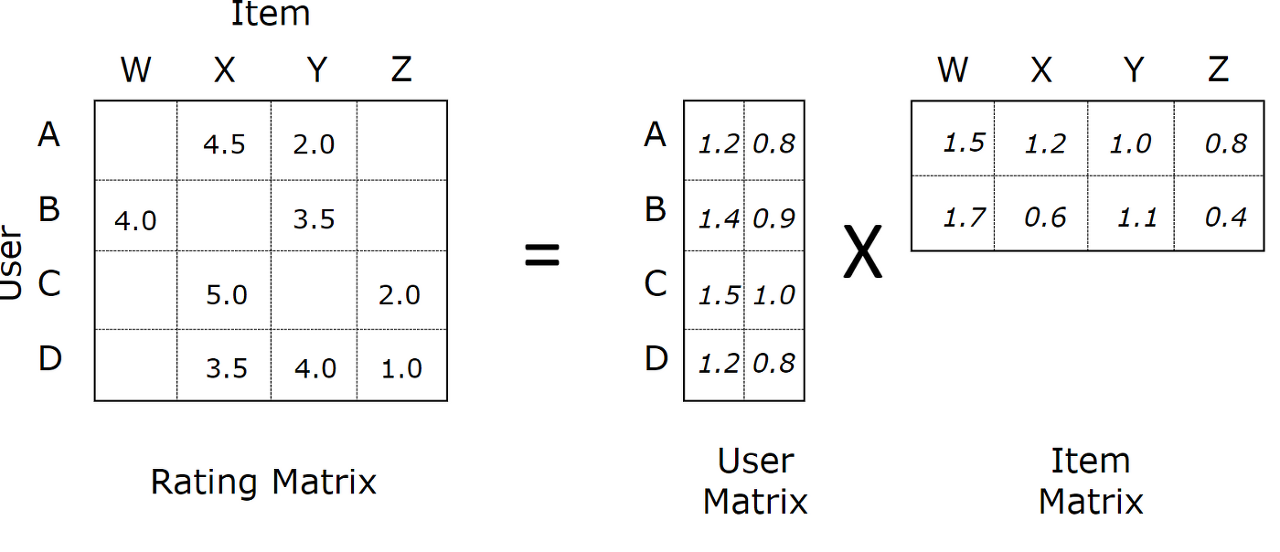
이러한 $m\times n$행렬을 2개로 분해하여 $m\times k$ 크기의 행렬과 $k\times n$ 크기의 행렬로 만든다면, 전자는 $m$명의 사용자들의 특성을, 그리고 후자는 $n$개의 상품들의 특성을 설명한다고 이해할 수 있다. 여기에서 $k$는 임의로 정할 수 있는 초매개변수이며, 모델의 수용력과 직접적으로 연관된다.

상호작용 행렬을 $R\in\mathbb{R}^{m\times n}$으로, 사용자의 정보를 담은 행렬을 $P\in \mathbb{R}^{m\times k}$로, 그리고 상품 정보를 담은 행렬을 $Q\in\mathbb{R}^{k\times n}$으로 정의해 보자. 위와 같이 빈칸이 있는 행렬 $R$이 주어졌을 때, 두 개의 행렬 $P$와 $Q$로 분해하는 것이 가능하다고 가정하면, 우리는 $P\times Q$를 계산하여 새로운 빈칸이 없는 행렬 $\hat{R}$을 만들 수 있다.

\[R\approx PQ = \hat{R}\]

이 행렬의 값들을 빈칸에 대한 예측으로 사용하는 것이 Matrix Factorization 기법의 아이디어이다. 넷플릭스 데이터셋에는 480,189명의 사용자와 17,770개의 영화가 존재하므로 실제 행렬은 이보다 훨씬 클 것이다. 하지만 기본적인 이론은 똑같이 적용할 수 있다.

SVD를 이용한 행렬 분해

행렬 $R$이 다음과 같이 주어졌다고 하자. 편의상 점수의 범위는 1점~3점으로 설정하였다.

우리는 이 행렬에 몇 개의 구멍을 뚫어 미관측된 데이터를 표현할 것이다. 이제 알고리즘을 통해 구멍이 뚫린 위치의 값을 얼마나 정확히 복원할 수 있는지 확인해 보자.

하지만 잠깐, $R$에는 빈칸이 있어서 SVD를 곧바로 적용하기가 곤란하다. 그렇기에 지금은 빈 칸을 0으로 채워넣고 진행하도록 한다. 물론 평균값으로 채워넣는 등 다른 외삽(extrapolation) 방법도 존재한다.

뭔가 찝찝하지만 우선은 계속 진행하겠다. 이 찝찝함은 나중에 돌아와서 살펴볼 것이다. 이제 SVD를 사용해서 행렬을 $U\times \Sigma\times V$형태로 분해할 수 있다. 우선 Full SVD를 사용해 보자.

주어진 $R$을 3개의 행렬로 분해했다. 이것은 곧 $R$을 2개의 행렬로 분해한 것이나 다름없다. 앞의 두 행렬, 혹은 뒤의 두 행렬을 곱해서 하나의 행렬로 만들어 버리면 되기 때문이다. 이제 행렬 분해의 결과를 다시 서로 곱해 $\hat{R}$을 계산해 보자.

이것으로 우리의 알고리즘은 nan이었던 값들을 모두 0으로 예측한 셈이 된다. 이것은 실제 정답인 $(1, 2, 1)$을 생각해 보면 형편없는 예측이다. 하지만 자세히 생각해 보면 우리는 구멍이 뚫린 부분의 값을 0으로 채워넣었다. 결국 이 예시에서 Full SVD를 사용한 Matrix Factorization은 외삽된 값까지 학습해버리기 때문에 일반화 성능이 떨어진다는 것이다. 오버피팅된 것이다.

Truncated SVD

오버피팅된 상태의 모델을 개선하는 간단한 방법으로는 수용력을 줄이는 것이 있다. 지금까지 사용한 Full SVD 대신 truncated SVD를 사용해, 2개의 특잇값(Singular Value)만을 사용한다면 다음과 같은 결과를 얻는다.

원본 행렬을 복원하는 능력은 조금 떨어지지만, 이번에는 $(1, 2, 1)$에 해당하는 값들을 각각 $(0.04, 0.08, -0.0.8)$로 예측하였다. 이전보다는 훨씬 나은 결과이다!

최적화 문제로의 변환

조금 더 고차원적인 해법을 찾기 위해 수학적인 접근을 시도해 보자. SVD에는 다음과 같은 아름다운 특징이 존재한다.

💡 에카르트-영 정리(Eckart-Young Theorm)
$R$을 $k$개의 특잇값을 사용해 행렬 $\hat{R}$로 근사했을 때, $X$가 임의의 $k$랭크 행렬이라면 $\hat{R}$은 다음을 만족한다.

\[\begin{align*} \min_{\text{rank}(X)\leq k} ||R-X||_2 &= ||R-\hat{R}||_2\\ \min_{\text{rank}(X)\leq k} ||R-X||_F &= ||R-\hat{R}||_F\\ \min_{\text{rank}(X)\leq k} ||R-X||_{Nuclear} &= ||R-\hat{R}||_{Nuclear}\\ \end{align*}\]

예를 들어 $k=5$의 truncated SVD로 $\hat{R}$을 계산했다면, 그 $\hat{R}$은 세상에 존재하는 그 어떤 랭크 5 이하의 행렬보다도 낮은 $||R-\hat{R}||_2$값을 제공한다. 따라서 $k$-truncated SVD를 통해 $\hat{R}$을 구하는 과정은, $\text{argmin}_{X, rank(X)\leq k}||R-X||_2$라는 최적화 문제를 푸는 과정과 수학적으로 완벽한 동치인 것이다! 그렇다면 주어진 문제는 다음과 같이 변환된다.

\[\min_{X, \text{rank}(X)\leq k}||R-X||_2\\ \min_{P,Q, \text{rank}(PQ)\leq k}||R-PQ||_2\\ \min_{p*, q*, \text{rank}(PQ)\le k}\sum^m_{i=1}\sum^n_{j=1}(r_{u, i}- {p_u}^\text{T} q_i)^2\]

이제 무엇이 문제인지 확실히 보인다. 세 번째 수식에는 행렬 $R$의 모든 원소에 대해서 최적화를 진행하는 과정이 드러나 있다. 그렇기 때문에 알고리즘은 행렬의 빈칸을 어떤 값으로 예측하는 대신, 임의로 채워넣은 0이라고 그대로 대답했던 것이다. 임의로 채워넣은 값을 학습에 사용하지 않도록 수식을 수정하면 다음과 같다.

\[P, Q = \text{argmin}_{p*, q*}\sum_{(i, j)\in \mathcal{K}}(r_{u, i}- {p_u}^\text{T} q_i)^2\]

이제 행렬 $P$와 $Q$를 무작위로 초기화한 뒤 경사 하강법을 이용해 최적화를 진행하면 된다. 이것이 추천 시스템에서 이용되는 Matrix Factorization 기법의 기본 형태이다.

Alternating Least Squares

이러한 방식의 Matrix Factorization 문제에는 경사하강법보다 월등히 효율적인 알고리즘이 존재한다. 그것이 ALS 알고리즘으로, $P$와 $Q$중 하나를 고정시킨 뒤 행렬 방정식을 수학적으로 해결하는 것을 반복하는 알고리즘이다.

주어진 목적함수를 잘 살펴보면 미지수가 2개로 non-convex함수라는 것을 알 수 있다. 따라서 이 함수는 해석학적으로 최소지점을 찾는 것이 어렵다. 하지만 두 미지수 중 하나를 상수로 취급한다면, Convex한 목적함수가 되어 단번에 최소지점을 찾을 수 있다. ALS 알고리즘의 장점은 다음과 같다.

• 경사하강법보다 수렴 속도가 월등히 빠르다.
• 매 반복마다 목적함수의 값을 반드시 감소시킬 것을 보장한다.
• 병렬화가 가능하다.

모델 개선

지금까지 추천 시스템에 사용되는 Matrix Factorization 모델의 기본 형태를 살펴보았다. 하지만 거금이 걸린 Netflix Prize 대회에서 우승을 거머쥐려면 훨씬 더 많은 노력이 필요하다. 벨코(BellKor)팀은 각종 수단을 총동원해 주어진 정보를 최대한 활용했다. 이 전략들은 모두 기본 모델에서 파생된 것으로, 원하는 대로 기본 모델에 추가 혹은 제거가 가능하다.

1. Regularization

\[\min_{q*, p*}\sum_{(u, i)\in \mathcal{K}} (r_{ui}-{p_u}^\text{T}q_i)^2+\lambda(||p_u||^2+||q_i||^2)\]

목적함수에 L2 정칙화 항을 추가했다. 이와 관련해서는 Deep Learning Book의 7챕터의 L2 정칙화 항목을 참고하면 좋다.

2. Adding Biases

\[\hat{r}_{ui}={p_u}^\text{T}q_i+b_u+b_i+\mu\]

사용자와 상품에는 각각 편향(bias)이 존재한다. 예를 들면 명작 영화 “타이타닉”은 대체로 높은 평가를 받는다. 어떤 사용자는 까다로워서 4~5점은 절대로 주지 않는다. 이러한 성격을 담아내고자 도입한 것이 바로 편향 파라미터이다. 결과적으로 모델의 파라미터가 늘어나게 되지만, 그만큼 수용력과 표현력이 상승한다. $b_u$는 사용자 편향 파라미터, $b_i$는 상품 편향 파라미터, $\mu$는 모든 평점의 평균을 나타내는 상수이다.

3. Temporal Dynamics

\[\hat{r}_{ui}(t)={p_u}^\text{T}q_i(t)+b_u(t)+b_i(t)+\mu\]

시간이 흐르면 사용자의 취향도 변한다. 따라서 각종 파라미터를 시간에 따라 변하도록 설정하는 아이디어가 바로 Temporal Dynamics이다. 이 경우 목적함수의 $\mu$를 제외한 모든 항이 시간 $t$에 대한 함수로 표현된다.

4. Confidence Levels

\[\min_{q*, p*}\sum_{(u, i)\in \mathcal{K}} c_{ui}(r_{ui}-{p_u}^\text{T}q_i)^2+\lambda(||p_u||^2+||q_i||^2)\]

Collaborative Filtering for Implicit Feedback Datasets에서 소개된 바로 그 기법이다. $c_{ui}$는 confidence를 나타내며, 사용자가 해당 상품과 몇 번이나 상호작용했는지를 세는 숫자이다. 이것으로 중복된 데이터를 버리지 않고 더 강한 선호도를 표현할 수 있게 된다. 평점 정보와 같은 명시적(Explicit) 데이터는 현실에서 좀처럼 찾아보기 힘들기에, 클릭 여부와 같은 암묵적(Implicit) 데이터를 가지고도 Matrix Factorization 기법을 활용할 수 있도록 목적함수를 개량한 것이다. 물론 Netflix Prize 대회에서는 명시적 데이터가 주어졌지만, 최대한 많은 정보를 활용하기 위해 유사한 기법을 사용한다.

5. Ensemble

정칙화 기법에 속한다. 이와 관련해서는 Deep Learning Book의 7챕터의 앙상블 기법 항목을 참고하면 좋다. 이들이 Netflix Prize 대회에 최종적으로 답안을 제출할 때는 무려 107개의 모델을 앙상블하여 내놓은 결과물을 사용했다고 한다.

포스트가 마음에 드셨다면, 좋아요를 남겨주세요!