[DL Book] 7-1-1. Parameter Norm Penalties, L2 Regularization

7.1.1. L2 파라미터 정칙화

L2 파라미터 정칙화는 정칙화 항을 모델 파라미터에 대한 L2 노름의 제곱의 절반으로 삼는 전략으로, 딥러닝 이전에도 릿지 회귀 혹은 티호노프 정칙화라는 이름으로 이미 널리 알려졌다. 편의를 위해 편향 파라미터가 없는 모델의 목적함수 $J$와 L2 정칙화가 적용된 목적함수 $\hat{J}$를 생각해 보자.

\[\begin{align*} \Omega(w)&=\color{red}{\frac{1}{2}\|w\|^2_2}\\ \tilde{J}(w;X,y) &=J(w;X,y) + \color{red}{\alpha(\frac{1}{2}\|w\|^2_2)}\\ &=J(w;X,y) + \color{red}{\frac{\alpha}{2}w^\text{T}w} \end{align*}\]

이 경우 파라미터 $w$에 대한 gradient는 다음과 같이 주어진다.

\[\nabla_w\tilde{J}(w;X,y)=\nabla_w J(w;X,y)+\color{red}{\alpha w}\]

그렇다면 학습률 $\epsilon$가 주어졌을 때 각 단계의 가중치 갱신 규칙은 다음과 같다.

\[\begin{align*} &w \leftarrow w-\epsilon(\textcolor{red}{\alpha w}+\nabla_wJ(w;X,y))\\ &w\leftarrow (1-\epsilon \textcolor{red}{\alpha})w-\epsilon\nabla_wJ(w;X,y) \end{align*}\]

정칙화를 적용하지 않은 갱신 규칙과 비교해 보면 그 차이가 확연히 드러난다.

\[\begin{align*} w&\leftarrow \hspace{2.1cm} w-\epsilon\nabla_wJ(w;X,y) \hspace{0.5cm}&\text{unregularized}\\ w&\leftarrow (1-\epsilon \textcolor{red}{\alpha})w-\epsilon\nabla_wJ(w;X,y) &\text{L2 regularized} \end{align*}\]

즉 $\alpha$는 가중치가 갱신될 때마다, gradient를 적용하기 직전에 가중치의 크기를 줄여 주는 역할을 함을 확인할 수 있다. 정확히는 양수, 음수를 불문하고 가중치의 절댓값을 작게 만든다.

하이퍼파라미터 $\boldsymbol \alpha$ 값의 중요성

이번에는 $\boldsymbol w^\ast$에서 목적함수 $J(\theta)$가 최솟값을 가진다고 가정하고, 테일러 급수를 이용해 $J(\theta)$를 분해해 보자. 테일러 급수의 전개는 무한히 계속될 수 있지만 2차항까지만 사용한다. 이것을 Quadratic Approximation이라고 한다.

\[\begin{align*} f(x)&=\sum^n_{k=0}\frac{f^{(k)}(a)}{k!}(x-a)^k \hspace{3.5cm}\text{Taylor Expansion} \\ &\approx f(a)+f'(a)(x-a)+\frac{1}{2!}f''(a)(x-a)^2+\textcolor{gray}{\frac{1}{3!}f'''(a)(x-a)^3 \cdots} \end{align*}\]

목적함수 $J(\theta)$를, 최솟값을 가지게 하는 지점 $\boldsymbol w^*$에서 2차 다항함수로 근사하면 다음과 같다.

\[\hat{J}(\theta)=J({\boldsymbol w}^\ast)+\color{lightgray}{J'(\boldsymbol{w^*})(\boldsymbol{w}-\boldsymbol{w}^\ast)+}\frac{1}{2}(\boldsymbol{w}-\boldsymbol{w}^\ast)\boldsymbol{H}(\boldsymbol{w}-\boldsymbol{w}^\ast)\]

2차 다항함수 근사에서는 일반적으로 함수 원형과 1차, 2차 도함수가 포함된 항을 남기는데, 정의상 $\boldsymbol{w}^\ast$는 최솟값이므로 $\boldsymbol{w}^\ast$에서의 1차 도함수는 0이 된다. 또한 최솟값이 존재함이 전제되므로 $\boldsymbol H$는 Positive Semi-Definite이어야 한다.

그러면 근사 목적함수 $\hat{J}(\theta)$는 그 미분이 0이 되는 곳에서 최솟값을 가진다.

\[\nabla_{\boldsymbol w}\hat{J}(\theta) = \boldsymbol{H}(\boldsymbol{w}-\boldsymbol{w}^\ast)=0\]

여기서 정칙화 항 $\Omega(\theta)=\frac{1}{2}||\theta||^2_2$ 를 도입한다고 생각해 보자. 그렇다면 방금 계산한 미분값에 정칙화 항의 미분값을 더해주어야 한다. 그 후, 수식을 0으로 만드는 $\boldsymbol{w}$를 찾으면 다음과 같다.

\[\begin{align*} \boldsymbol{H}(\boldsymbol{w}-\boldsymbol{w}^\ast)+\textcolor{red}{\alpha\boldsymbol{w}} &=0\\ (\boldsymbol{H}+\textcolor{red}{\alpha\boldsymbol{I}})\tilde{\boldsymbol{w}}&=\boldsymbol{H}\boldsymbol{w}^\ast\\ \tilde{\boldsymbol{w}}&=(\boldsymbol{H}+\textcolor{red}{\alpha\boldsymbol{I}})^{-1}\boldsymbol{H}\boldsymbol{w}^\ast \end{align*}\]

여기서 우선적으로 확인할 수 있는 것은, $\alpha$가 0에 무한히 가까워질수록 정칙화의 효과가 사라지며, 결국 정칙화된 목적함수의 최적화 해는 $\tilde{\boldsymbol{w}}=\boldsymbol{HH^{-1}}\boldsymbol{w}^\ast$가 되어, 정칙화되지 않은 목적함수의 최솟값으로 정의된 $\boldsymbol{w}^\ast$ 와 같아진다는 것이다.

하이퍼파라미터 $\boldsymbol \alpha$ 값의 의미

계속해서 $\boldsymbol{H}$는 헤시안 행렬로 대칭행렬이며, 고윳값 분해가 가능하다. $\boldsymbol{H=Q\Lambda Q}^{\text{T}}$로 고윳값 분해를 진행하고 수식을 정리하면,

\[\begin{align*} \boldsymbol{\tilde{w}}&=(\boldsymbol{Q\Lambda Q}^{\text{T}}+\alpha\boldsymbol{I})^{-1}\boldsymbol{Q\Lambda Q}^{\text{T}}\boldsymbol{w}^\ast\\ &=\bigg[\boldsymbol{Q(\Lambda}+\alpha {\boldsymbol I}) \boldsymbol{Q}^{\text{T}}\bigg]^{-1}\boldsymbol{Q\Lambda Q}^{\text{T}}\boldsymbol{w}^\ast\\ &=\color{blue}{\boldsymbol Q}\color{green}{(\Lambda}\color{green}{+\alpha{\boldsymbol I})^{-1} {\boldsymbol \Lambda}}\color{blue}{\boldsymbol Q^{\text{T}}}\boldsymbol{w}^\ast \end{align*}\]

고윳값 분해의 $\boldsymbol{\color{blue}Q\color{green}\Lambda \color{blue}{Q^{\text{T}}}}$의 각 행렬은 각각 회전→크기변환→회전의 과정을 나타낸 것으로 해석할 수 있다. 여기에서 L2 정칙화의 효과를 엿볼 수 있다.

💡 자세히 보기:

L2 정칙화를 적용하면 기존 최적화 해 $\boldsymbol w^\ast$가 새로운 점 $\tilde{\boldsymbol w}$로 이동한다.

• 기존 최적화 해 $\boldsymbol w^\ast$는 $\boldsymbol H$의 고유벡터의 방향으로 선형변환되며, 그 크기가 조절되는 정도는 $\boldsymbol H$의 고윳값들과 연관이 있다.
• L2 정칙화를 시행하면 고윳값들에 $\alpha$만큼의 상수가 더해진다. 따라서,
  • $\alpha$보다 작은 고윳값들은 그만큼 영향을 많이 받는다. 즉 해당 고유벡터 방향으로는 큰 변환이 일어난다.
  • $\alpha$보다 큰 고윳값들은 비교적 영향을 덜 받는다. 즉 해당 고유벡터 방향으로는 작은 변환만이 일어난다.

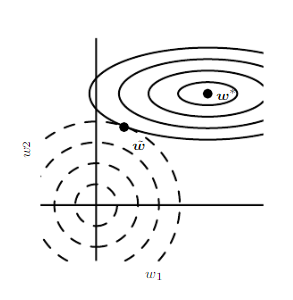
L2 정칙화의 기하학적 의미

위 그림에서 $\boldsymbol w^\ast$는 원본 목적함수 $J$를 최소화시키는 지점이고, 원점 $(0, 0)$은 정칙화 항 $\alpha \times \frac{1}{2}||\boldsymbol w||^2_2$ 를 최소화시키는 지점이다. L2 정칙화된 목적함수 $\hat{J}$는 양쪽 모두를 최소화시켜야 하므로, 두 함수가 점점 바깥으로 뻗어나가다가 만나는 지점에서 최솟값을 가지게 된다.

포스트가 마음에 드셨다면, 좋아요를 남겨주세요!