[DL Book] 7-1-1. Parameter Norm Penalties, L1 Regularization

7.1.2. L1 정칙화

L2 정칙화는 가중치 감쇠(weight decay)의 가장 흔한 형태이지만 다른 형태의 정칙화도 존재한다. 대표적인 전략으로 L1 정칙화가 있다. L1 정칙화는 입력값의 각 원소의 절댓값의 합으로 정의된다.

\[\Omega(\theta)=\|\boldsymbol w\|_1=\sum|\boldsymbol{w}_i|\]

마찬가지로 편향 파라미터가 없는 선형회귀 문제를 L1 정칙화를 이용해 풀어 보자. 일반적인 목적함수가 $J$로 주어진다면 L1 정칙화가 적용된 목적함수 $\tilde{J}$는 다음과 같이 정의된다.

\[\tilde{J}(\boldsymbol w;\boldsymbol X,\boldsymbol y)=J(\boldsymbol w;\boldsymbol X,\boldsymbol y)+\color{red}{\alpha\|\boldsymbol w\|_1}\]

또한 그 Gradient는 다음과 같이 정의된다. 위에서 살펴본 L2 정칙화와 비교하면 다른 부분이 보인다. L2 정칙화의 경우는 파라미터 $\boldsymbol w$가 상수배가 되어 곧바로 Gradient에 영향을 미친다. 반면 L1 정칙화의 경우 파라미터가 보다 간접적인 영향을 미친다. 또한, $\text{sign}$함수의 특성상 이 Gradient를 가지고 해석학적 분석을 진행하는 데에는 한계가 있다.

\[\begin{align*} \nabla_{\boldsymbol w}\tilde{J}(\boldsymbol w;\boldsymbol X, \boldsymbol y)&=\nabla_{\boldsymbol w}J(\boldsymbol X,\boldsymbol y;\boldsymbol w)+\color{red}{\alpha \text{sign}({\boldsymbol w})}\hspace{0.5cm}&\text{L1 regularization} \\ \nabla_{\boldsymbol w}\tilde{J}(\boldsymbol w;\boldsymbol X,\boldsymbol y)&=\nabla_{\boldsymbol w} J(\boldsymbol w;\boldsymbol X,\boldsymbol y)+\color{red}{\alpha {\boldsymbol w}} \hspace{0.5cm}&\text{L1 regularization} \end{align*}\]

하이퍼파라미터 $\boldsymbol \alpha$ 값의 중요성과 의미

L2 정칙화에서 살펴본 것과 같은 방법으로 Quadratic Approximation을 통한 분석을 진행해 보자. 원본 목적함수 $J$를 Quadratic Approximation을 통해 근사한 $\hat{J}$는 다음과 같이 표현된다.

\[\hat{J}(\theta)=J({\boldsymbol w}^\ast)+\color{gray}{J'(\boldsymbol{w^\ast})(\boldsymbol{w}-\boldsymbol{w}^\ast)}+\frac{1}{2}(\boldsymbol{w}-\boldsymbol{w}^\ast)\boldsymbol{H}(\boldsymbol{w}-\boldsymbol{w}^ast)\]

마찬가지로 $\boldsymbol w^*$는 $J$가 최솟값을 가지는 점으로 정의되었기에 $J’(\boldsymbol w^\ast)=0$이 되고, 1차항이 사라진다. 이렇게 근사한 목적함수 $\hat{J}$의 Gradient는 다음과 같다.

\[\nabla_{\boldsymbol w}\hat{J}(\theta) = \boldsymbol{H}(\boldsymbol{w}-\boldsymbol{w}^\ast)\]

여기에서 $\boldsymbol H$는 $\boldsymbol{w=w^\ast}$에서 평가한 $J(\boldsymbol w)$의 헤세 행렬이다. $\text{sign}$함수와의 계산을 용이하게 하기 위해서 $\boldsymbol H$가 모든 원소가 양수인 대각행렬이라고 가정하자.

이제 정칙화 항 $\color{red}{\alpha|\boldsymbol w|_1}$을 $\hat{J}$에 더해, L1 정칙화된 형태의 $\hat{J}$를 얻을 수 있다.

\[\begin{align*} \hat{J}(\boldsymbol w)&=J(\boldsymbol w^\ast)+\frac{1}{2}(\boldsymbol{w-w^\ast})\boldsymbol{H}(\boldsymbol{w-w^\ast}) +\color{red}{\alpha|w|_1}\\ &=J(\boldsymbol w^\ast)+\sum_i\bigg[\frac{1}{2}H_{i, i}(\boldsymbol{w-w^\ast})^2 + \textcolor{red}{\alpha|w_i|}\bigg] \end{align*}\]

이렇게 정리된 $\hat{J}$는 해석적으로 최솟값을 가지는 위치를 찾을 수 있다. $\boldsymbol w$의 각 원소가 다음과 같을 때, $\hat{J}$는 최솟값을 가진다.

\[w_i=\text{sign}(w_i^\ast)\max\bigg\{\left|w_i^\ast\right|-\frac{\alpha}{H_{i, i}}, 0\bigg\}\]

• $|w_i^*|<=\frac{\alpha}{H_{i, i}}$인 경우, $i$번째 차원의 최적화 해 $w_i$는 0이 된다.
  이는 L1 정칙화의 효과가 강하게 작용해, 최적해가 되는 점을 원점에 가까워지도록 끌어당긴 것으로 해석할 수 있다.

• $|w_i^\ast|>\frac{\alpha}{H_{i, i}}$인 경우, $i$번째 차원의 최적화 해 $w_i$의 크기는 $\alpha$에 비례해 약간 작아진다.
  이는 L1 정칙화가 작용했지만, 원점으로 끌고 갈 만큼 강한 효과가 작용하지는 않은 것으로 바라볼 수 있다.

L1 정칙화와 희소성(Sparsity)

위 수식에서도 살펴보았듯이 L1 정칙화의 특징은 해의 많은 값을 0으로 만든다는 것이다. 이러한 희소성(Sparsity)은 L1 정칙화가 L2 정칙화와는 다른 독특한 성질을 띠게 한다.

예를 들면 L2 정칙화된 목적함수의 해에서 출발해, 위에서 헤세 행렬에 적용했던 가정을 똑같이 적용할 수 있다. 그러면 $\boldsymbol H=diag([H_{1, 1},\cdots,H_{n, n}])$이면서 $H_{i, i} > 0$이 되고, L2 정칙화된 목적함수는 다음과 같은 $\boldsymbol w$에서 최솟값을 가질 것이다.

\[\tilde{w}_i=\frac{H_{i, i}}{H_{i, i}+\alpha}w_i^\ast\]

여기서 눈치챌 수 있는 것은 L2 최적화의 경우 $w^\ast_i$가 0인 경우를 제외하면 $\tilde{w}_i$를 절대로 원점까지 끌고 가지 않는다는 것이다. 반면, L1 최적화의 경우 $\max(x, 0)$이 등장하는 까닭에 L2 norm의 경우보다 훨씬 더 많은 값을 원점으로 끌고 가게 된다.

L1 정칙화의 기하학적 의미

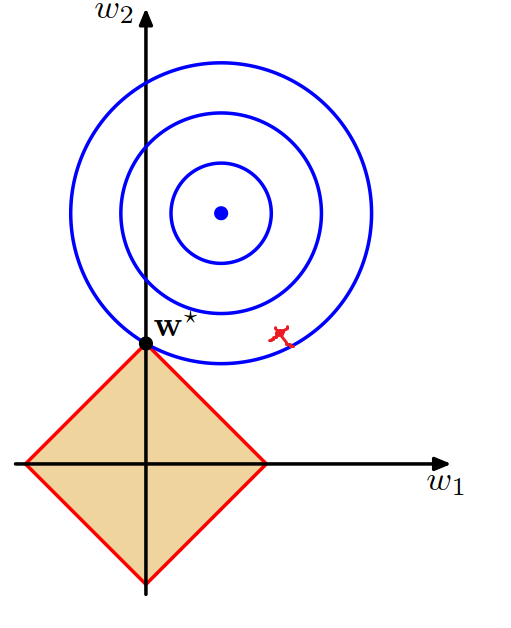
L2 정칙화에서 살펴본 것처럼, 목적함수 $\color{blue}J$와 원점을 중심으로 하는 정칙화 항 $\color{red}{\alpha|\boldsymbol w|_1}$의 합으로 이루어진 함수 $\hat{J}$는 $\color{blue}J$와 $\color{red}{\alpha|\boldsymbol w|_1}$가 만나는 지점에서 최솟값을 가진다. L2 정칙화와의 차이점은 L1 정칙화의 경우 목적함수의 영역이 원형이 아닌 선형적으로 정의된다는 것이며, 이로 인해 $x$ 절편과 $y$ 절편에서 뾰족한 형태를 띠게 된다.

이 뾰족함 때문에 $\color{blue}J$와 $\color{red}{\alpha|\boldsymbol w|_1}$의 접점은 $x$축 혹은 $y$축 상에서 생길 가능성이 L2 정칙화에 비해 높으며, 이것이 L1 정칙화의 희소성의 근원이라고 해석할 수 있다.

LASSO Regression에서

라쏘(Least Absolute Shrinkage and Selection Operator, LASSO) 회귀에서는 L1 정칙화를 도입함으로써 Feature Selection 효과를 누린다. L1 정칙화의 특성상 많은 파라미터를 0으로 보내는데, 이 파라미터들에 대응하는 Feature는 무의미한 것으로 간주할 수 있다는 것이다.

MAP Bayesian Inference 와의 관계

사후확률을 최대화하는 Maximum a Posteriori 추론은 다음과 같이 진행된다.

\[\begin{align*} \boldsymbol \theta \text{ with the highest posterior probability}&= \boldsymbol \theta_{\text{MAP}}\\ &=\underset{\theta}{\text{arg max}} \ p(\boldsymbol{\theta}|{\boldsymbol x})\\ &=\underset{\theta}{\text{arg max}}\big[\log p(\boldsymbol{x|\theta})\textcolor{red}{+ \log p(\boldsymbol \theta)}\big]\\ &=\underset{\theta}{\text{arg min}}\big[\textcolor{blue}{-\log p(\boldsymbol x|\boldsymbol \theta)}\textcolor{red}{-\log p(\boldsymbol \theta)}] \end{align*}\]

여기에서 로그 사전분포에 해당하는 항이 바로 정칙화와 연관이 있다. 예를 들면 라플라스 분포를 가중치의 사전분포로 잡는다면 음의 로그 사전분포는 다음과 같다.

\[\begin{align*} -\log p(\boldsymbol w)&=-\sum_i\log\text{Laplace}(w_i;0, \frac{1}{\alpha})\\&=\textcolor{red}{\alpha\|\boldsymbol w\|_1}-n\log\alpha+n\log 2 \end{align*}\]

여기에서 $\boldsymbol w$와 관계없는 항을 지워내면 L1 정칙화와 같아진다. 딥러닝에서는 Cross-Entropy를 손실함수로 자주 사용하는데, 이것은 곧 Negative Log Likelihood를 최소화하는 것과 동치임이 알려져 있다(PRML Section 4.3.4).

\[\begin{align*} &\underset{\theta}{\text{arg min}}\big[\textcolor{blue}{-\log p(\boldsymbol x|\boldsymbol \theta)}\textcolor{red}{-\log p(\boldsymbol \theta)}\big]\\ = \ &\underset{\theta}{\text{arg min}}\big[\textcolor{blue}{\text{Negative Log Likelihood}}+\textcolor{red}{\text{L1 Regularization}}\big] \end{align*}\]

즉 Cross-Entropy를 목적함수로 가지는 모델에 L1 정칙화를 도입하는 것은, 가중치의 사전분포를 라플라스 분포로 잡는 것과 같다. 마찬가지로 L2 정칙화를 도입하는 것은 가중치의 사전분포를 가우시안으로 잡는 것과 같다.

포스트가 마음에 드셨다면, 좋아요를 남겨주세요!