[DL Book] 7-8. Early Stopping

7.8. Early Stopping

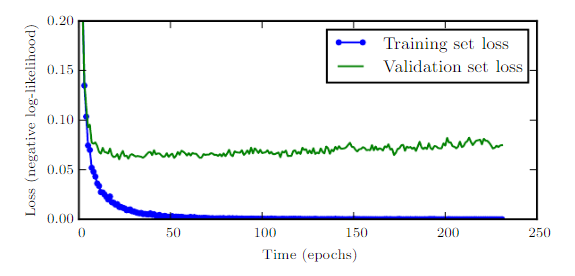
모델을 학습시키다 보면, 훈련 오차율은 계속해서 내려가지만 검증 오차율은 어느 지점을 넘어서면 더 이상 내려가지 않고 거꾸로 올라가기까지 한다. 이것은 모델이 훈련 데이터에 대해 오버피팅되고 일반화 성능을 잃기 때문이다.

그렇다면 우리는 관측된 검증 오차율이 가장 낮은 시점으로 되돌아가 그 때의 모델이 최고라고 선언할 수 있다. 엔지니어링적인 측면에서, 이것은 최소 검증 오차율이 갱신될 때마다 그 시점의 모델 가중치를 별도로 저장한 뒤, 학습이 종료된 후 가장 마지막으로 저장된 모델 가중치를 사용하는 것으로 구현이 가능하다.

이 전략을 조기 종료(Early Stopping)라고 부르며, 그 간단함과 강력함 덕분에 가장 대중화된 정칙화 기법 중 하나이다.

장점

• 매우 효율적인 하이퍼파라미터 탐색 학습에 사용되는 에폭(Epoch) 숫자는 어떤 관점에서는 하이퍼파라미터이다. 하지만 훈련을 여러 번 해야 하는 일반적인 하이퍼파라미터와는 반대로, 에폭 숫자는 단 한 번의 훈련으로 최적의 지점을 찾아낼 수 있다.
• 학습 과정에 영향을 미치지 않는다. L2 정칙화 등의 전략은 모델 파라미터의 학습 과정에 수치적으로 영향을 미친다. 따라서 잘못된 정칙화 전략을 선택하면 모델의 성능에 악영향을 미칠 수 있다. 반면 학습 조기종료는 도입 유무에 따른 학습 과정의 변화가 일절 존재하지 않는다.
• 다른 정칙화 전략과 함께 사용할 수 있다. 조기종료를 사용한다고 해서 무조건 모델이 Global Minimum으로 수렴하는 것은 아니다. 따라서 기타 정칙화 전략과 함께 사용하는 것이 권장되는데, 대다수의 정칙화 전략은 조기종료와 함께 사용하는 것이 가능하다.

단점

• 주기적으로 일반화 성능 확인이 필요하다. 학습 조기종료는 $n$ 에폭마다 검증 데이터셋을 기반으로 모델을 평가하고, 그 평가된 성능이 더 이상 성능이 증가하지 않을 때 학습을 멈추어야 한다. 이 때, 모델을 평가하는 과정에서 추가적인 컴퓨팅 자원의 소모가 발생한다.
  • 해결책 : 별도의 장치에서 병렬적으로 검증을 진행할 수 있다. 이 경우 시간적인 여유가 확보되므로 더 저렴한 장치(e.g. CPU)를 사용해도 좋다. 검증을 병렬로 진행할 수 없다면 검증 데이터셋의 크기를 작게 설정하는 등으로 시간 소모를 단축할 수 있다.
• 모델 파라미터를 기록하기 위한 저장공간이 별도로 필요하다. 하지만 이것은 일반적으로 큰 문제가 되지 않는다.
  • 해결책 : 정말로 자원의 효율적인 배분이 중요하다면, 학습에 사용되는 것(e.g. GPU 메모리)보다는 저렴하고 느린 장치(e.g. CPU 메모리, 하드 디스크)를 사용하는 것이 가능하다.
• 테스트 데이터셋 이외에 검증 데이터셋이 필요하다. 이것은 궁극적으로 학습에 사용할 수 있는 데이터가 적어짐을 의미한다.
  • 해결책 1 : 학습 조기종료로 최적의 에폭 숫자 $n$을 알아낸 뒤, 모든 데이터를 가지고 다시 $n$에폭만큼 학습한다. 단, 입력 데이터가 변했기 때문에 이전과 동일하게 최적의 모델을 학습할지는 정확히 알 수 없다.

  • 해결책 2 : 학습이 조기종료된 뒤 훈련 오차를 계산한다. 이후 검증 오차가 훈련 오차 아래로 내려갈 때까지, 전체 데이터를 사용해 훈련한다. 이 알고리즘은 매우 불안정하며 유한 시간 내에 종료되지 않을 수도 있다.

    
    💡 yellokat의 말:
    이 방법은 정말 듣기만 해도 그지같은 방법인데 이게 정말 좋은 방법인지 잘 모르겠네요…

학습 조기종료의 해석적 특징

L1과 L2 정칙화에서 소개한 것처럼, 목적함수 $J(\boldsymbol w)$와 그것이 최솟값을 가지게 하는 지점 $\boldsymbol w*$에서 이차함수로 근사한 수식 $\hat{J}(\boldsymbol w)$를 살펴보자.

\[\hat{J}(\boldsymbol w)=J(\boldsymbol w^\ast)+\frac{1}{2}(\boldsymbol w-\boldsymbol w^\ast)^{\text{T}}\boldsymbol H (\boldsymbol w-\boldsymbol w^\ast)\]

여기에서 $\boldsymbol H$는 $\boldsymbol w^\ast$에서 평가한 $J(\boldsymbol w)$의 헤세 행렬이며, $J(\boldsymbol w)$가 $\boldsymbol w^\ast$에서 최솟값을 가짐이 정의되었으므로 $\boldsymbol H$는 준정부호행렬(Positive Semi-Definite)이다. 이렇게 근사한 $\hat{J}$의 Gradient는 다음과 같다.

\[\nabla_{\boldsymbol w} \hat{J}(\boldsymbol w)=\boldsymbol H(\boldsymbol w-\boldsymbol w^\ast)\]

그러면 각 스텝 $\tau$에서 파라미터 업데이트는 다음과 같이 이루어진다.

\[\begin{align*} \boldsymbol w^{(\tau)}&= \boldsymbol w^{(\tau-1)}-\epsilon\nabla_{\boldsymbol w}\hat{J}(\boldsymbol w^{(\tau-1)})\\ &= \boldsymbol w^{(\tau-1)}-\epsilon\boldsymbol H(\boldsymbol w^{(\tau-1)}-\boldsymbol w^*) \end{align*}\]

이 수식을 정리하고, $\boldsymbol H$의 고윳값 분해를 이용하여 $\boldsymbol H=\boldsymbol Q\boldsymbol \Lambda \boldsymbol Q^{\text{T}}$를 대입한다.

\[\begin{align*} \boldsymbol w^{(\tau)}-\boldsymbol w^\ast &=(\boldsymbol I -\epsilon\boldsymbol H)(\boldsymbol w^{(\tau-1)}-\boldsymbol w^\ast)\\ \boldsymbol w^{(\tau)}-\boldsymbol w^\ast &=(\boldsymbol I -\epsilon\boldsymbol Q\boldsymbol \Lambda \boldsymbol Q^{\text{T}})(\boldsymbol w^{(\tau-1)}-\boldsymbol w^\ast)\\ Q^{\text{T}}(\boldsymbol w^{(\tau)}-\boldsymbol w^\ast )&=(\boldsymbol I -\epsilon\boldsymbol \Lambda )Q^{\text{T}}(\boldsymbol w^{(\tau-1)}-\boldsymbol w^\ast)) \end{align*}\]

편의상 경사하강법을 원점에서 시작했다고 가정하면, $\boldsymbol w^{(0)}=0$이다. 또한 $\epsilon$은 매우 작은 수로 설정하여, $|1-\epsilon \lambda _i|<1$을 만족한다고 생각해 보자. 그렇다면 임의의 $\tau$시점에서 $\boldsymbol w$의 위치는 다음과 같다.

\[\boldsymbol Q^{\text{T}}\boldsymbol w^{(\tau)}=[\boldsymbol I-\textcolor{blue}{(\boldsymbol I-\epsilon\boldsymbol \Lambda)^{\tau}}]\boldsymbol Q^{\text{T}}\boldsymbol w^\ast \hspace{1.5cm}\text{Early stopping}\]

L2 정칙화와의 비교

그리고 이것을 L2 정칙화에서 살펴보았던, $\tilde{\boldsymbol w}$의 수식과 비교해 보자. 뒤돌아보자면, 이 수식은 마찬가지로 원본 목적함수 $J$와 그것이 최솟값을 가지게 하는 점 $\boldsymbol w^\ast$이 존재할 때, $J$를 $\boldsymbol w=\boldsymbol w^\ast$에서 이차함수로 근사한 함수 $\hat{J}$를 L2 정칙화한 뒤 다시 최솟값을 구한 것이다.

\[\begin{align*} \boldsymbol{\tilde{w}}&=\boldsymbol{Q (\Lambda}+\alpha{\boldsymbol I})^{-1} {\boldsymbol \Lambda} {\boldsymbol Q}^{\text{T}}\boldsymbol{w}^\ast\\ \boldsymbol Q^{\text{T}}\boldsymbol{\tilde{w}}&=\boldsymbol{ (\Lambda}+\alpha{\boldsymbol I})^{-1} {\boldsymbol \Lambda} {\boldsymbol Q}^{\text{T}}\boldsymbol{w}^\ast \\&=[\boldsymbol I-\textcolor{green}{(\boldsymbol \Lambda +\alpha\boldsymbol I)^{-1}\alpha}]\boldsymbol Q^\text{T}\boldsymbol w^\ast \hspace{1.5cm}\text{L2 Regularization} \end{align*}\]

그렇다면 만약 하이퍼파라미터 $\epsilon$, $\alpha$, $\tau$가 $\textcolor{blue}{(\boldsymbol I-\epsilon\boldsymbol\Lambda)^\tau}=\textcolor{green}{(\boldsymbol\Lambda+\alpha\boldsymbol I)^{-1}\alpha}$를 만족하도록 선택된다면, 두 수식은 수학적으로 동치가 된다. 어떤 시각에서는 학습 조기종료가 L2 정칙화의 일반화일 수 있는 것이다. 그러나 두 정칙화 방식은 동일선상에 놓기 어렵다. 검증 데이터셋을 두고 주기적으로 평가한다는 특성상, 학습 조기종료는 L2 정칙화를 통해 얻을 수 있는 최적해보다도 더 좋은 일반화 성능을 제공하는 sweet spot을 발견할 수 있는 잠재력을 가지고 있다.

포스트가 마음에 드셨다면, 좋아요를 남겨주세요!